Research Update 3/15/16

Can anyone really keep log and linear domains separate? Probably, but it's not me. Got my domains mixed up, specifically I converted from a single ended to double ended FFT spectrum by doubling. This works in the linear area, but not in dB domain. Fixed my mistake by doubling then taking the log() of it. Now we're back to the expected single pole system performance.

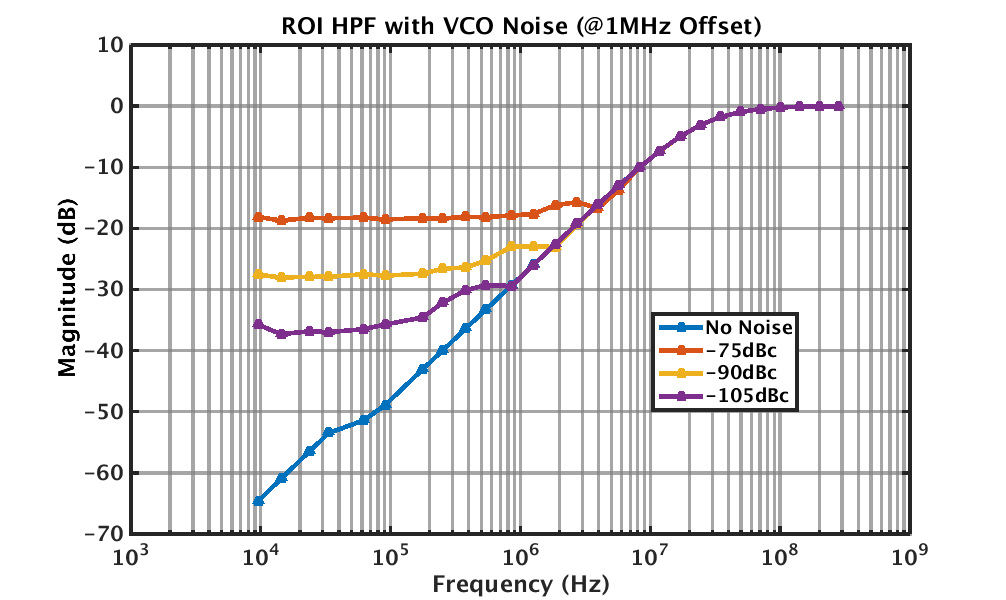
VCO noise is a hard limiter on system performance currently. At low frequencies, VCO noise dominates the curve, which means we can't “roll off” any further. Going to investigate choppers and modulators and resonators [oh my] as possible solutions.

This is nice, but I need to do the actual math on loop simulations. A rough hack at it below:

$$ NTF_{in} = \dfrac{1}{1+k_r \frac{I_{cp}}{\pi} \frac{k_{vco}}{s}} = \dfrac{s}{s+k_r\frac{I_{cp}}{\pi}k_{vco}} $$

$$ NTF_{vco} = \dfrac{k_r I_{cp}}{\pi} NTF_{in} $$

$$ NTF_{cp} = k_r NTF_{in} $$

$$ NTF_{R} = NTF{in} $$

Where $ NTF_x $ is the noise transfer function from node $x$ to the output.